陶哲轩转发！华人数学博士后反超DeepMind AI，停滞18年数学问题1个月内3次突破

数学家出手反击 AI！对 AlphaEvolve 在 " 集合和差问题 " 上的成果进一步改进。

DeepMind 于 5 月 14 日宣布 AlphaEvolve，不仅改进了矩阵乘法算法，还取得一系列成果，打破集合和差问题（Sums and differences of sets problem）自 2007 年来的纪录也是其中之一。

这一次，人类方法使用测度集中性来计算渐近值，只需要少量的计算机辅助。

不到一个月时间，这个停滞 18 年的问题在人类与 AI 共同努力下 3 次取得突破。

陶哲轩转发评价道：

对我来说，这生动展示了处理数学问题时，大量计算机辅助、适度计算机辅助和传统 " 纸笔 " 方法未来的相互作用，这些模式各有优缺点。

例如当前的 AlphaEvolve 很难处理后续论文中使用的渐近构造。

但另一方面，如果不先进行类似 AlphaEvolve 的半自动化搜索，人类方法也很难找到这些改进的机会。

最新成果来自西班牙数学科学研究所 ICMAT 的博士后 Fan Zheng，

这次他通过构造一系列特殊的集合 U，在极限情况下将集合和差问题 θ 的下界提升至 1.173077。

集合和差问题是集合论领域一个经典问题。

对于于两个整数集合 A 和 B，它们的 " 和集 "（A+B）是所有可能的两数之和构成的集合，" 差集 "（A-B）是所有可能的两数之差构成的集合。

研究者想知道：当和集的大小被限制为不超过 K 倍 A 的大小时（即 | A+B| ≤ K|A|），差集的大小至少能有多大？

这个问题可以用一个指数 θ 来衡量，即差集大小至少是和集大小的 θ 次方级别（|A-B| ≥ c ( K ) ・|A+B|^ θ）。

θ 越大，说明在和集大小被限制的情况下，差集的大小下限越高。提升 θ 的下界是该领域研究者的核心目标之一。

AlphaEvolve 做了什么 ?

AlphaEvolve 针对这个问题的解法比较暴力，先让 Gemini 大模型生成成百上千种候选方案，再通过自动化评估系统筛选。

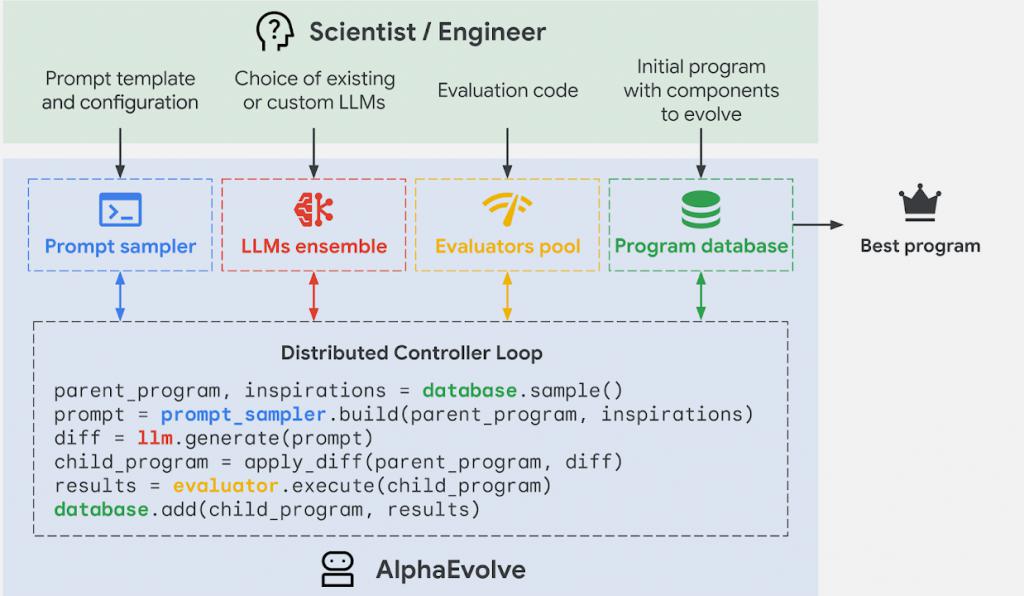
AlphaEvolve 采用了基于进化算法的框架，先用 Gemini 大模型生成的算法来构造满足条件的整数集合 U，自动化评估系统计算以下内容：集合 U 的大小、和集 |U+U| 的大小、差集 |U-U| 的大小、相应的 θ 值。

表现优异的算法被保留、变异或组合，投入下一轮优化。这个过程持续迭代，直到算法性能不再提升。

最终构造出一个包含 54265 个整数的集合，将 θ 的下界提高到 1.1584，比 18 年前的结果 1.14465 提高不少。

正如陶哲轩所说，AlphaEvolve 的结果激发了更多后续研究。

人类数学家如何改进？

首先出手的是匈牙利数学家 Robert Gerbicz。

他曾创建同名的 Gerbicz 错误检查方法，被 GIMPS 和 PrimeGrid 等项目用于 Proth 质数、 Mersenne 质数、Riesel 质数等问题的检查。

这一次针对集合和差问题，Gerbicz 引入坐标上界 B，将原本的集合 V ( m,L ) 重新定义成 W ( m,L,B ) 。

但新构造的集合既有和的约束（坐标和≤ L），又有单个坐标的约束（每个坐标≤ B），直接计算非常困难。

对于这一点，他利用组合数学中的容斥原理避免重复计算，先计算只有和约束的情况，再减去违反坐标约束的情况，最后考虑重叠部分的修正。

最终找到最优参数组合 m=81411，L=65536，B=5，构造出构造出超过 10^43546 个元素的超大集合。

在这个问题上，大集合的离散误差的相对影响减小，能更好地逼近连续情况下的理论极限，还允许更大的参数选择空间，避免免小数效应导致的次优解。

他利用这个集合计算出对应的 θ =1.173050，超越了 AlphaEvolve 的 θ = 1.1584。

他使用免费的 GMP 库，整个计算过程约需 15 小时，相关代码 Gerbicz 也开源在了 GitHub 上。

仅仅 10 天后，Fan Zheng 再次改进这个结果到 θ =1.173077。

虽然从 θ =1.173050 到 θ =1.173077 的提升看似微小，但他的主要贡献在于从具体构造转向理论分析。

在 Gerbicz 结果的基础上，Fan Zheng 又引入了大偏差估计（Large Deviation Estimates）作为渐近分析框架。分析当 m 和 L 很大时，集合 W ( m,L,B ) 的大小在极限情况下的规律。

Fan Zheng 的成果不仅在理论框架下获得的严格下界，还证明了通过渐近分析可以超越具体构造的限制，为进一步改进提供了系统性的方法。

对于这一系列成果，陶哲轩认为不应简单的看成是人类和 AI 谁赢谁输的零和博弈。

AlphaEvolve 方法的优势更多地在于广度而非深度；

人们可以使用 AlphaEvolve 扫描大范围的问题，以找出文献中可以改进的地方，然后人类专家（或许还会借助计算机）可以集中精力解决这些问题，取得进一步的进展。

不同的方法能够相互补充，从而推动数学进步，这本身就很棒。

Robert Gerbicz 论文：

https://arxiv.org/abs/2505.16105

Fan Zheng 论文：

https://arxiv.org/abs/2506.01896

参考链接：

[ 1 ] https://mathstodon.xyz/@tao/114619972458310957

—  完  —

 量子位 AI 主题策划正在征集中！欢迎参与专题365 行 AI 落地方案，一千零一个 AI 应用，或与我们分享你在寻找的 AI 产品，或发现的AI 新动向。

也欢迎你加入量子位每日 AI 交流群，一起来畅聊 AI 吧～

一键关注 点亮星标

科技前沿进展每日见

一键三连「点赞」「转发」「小心心」

欢迎在评论区留下你的想法！