揭开大模型“伪遗忘”,港理工等团队:结构不变就是没忘
近年来,大语言模型(LLMs)的能力突飞猛进,但随之而来的隐私风险也逐渐浮出水面。
训练中暴露的敏感信息往往被模型 " 记住 ",引发广泛关注。
在此背景下,机器遗忘(Machine Unlearning)技术应运而生,目标是在不影响整体能力的前提下,有选择性地抹除特定知识。
来自香港理工大学、卡内基梅隆大学和加州大学圣克鲁兹分校的研究团队通过构建一套表示空间的诊断工具,系统性地区分了" 可逆性遗忘 " 与 " 灾难性不可逆遗忘 ",并首次揭示了遗忘现象背后的表示结构变化规律——
真正的遗忘只有在多个网络层发生协同且大幅度扰动时才会出现;而相比之下,在高敏感区域(如输出 logits)中进行轻微更新虽然会显著降低准确率或提高困惑度,但模型内部表示结构仍可保持完整。
研究人员整理成了一个统一的表示层分析工具箱,支持诊断 LLM 在 Unlearning/Relearning/Finetuning 等过程中的内在变化。

真正的遗忘,是结构性的抹除,而非行为的抑制
研究者提出:" 一个模型若仅仅在 token 输出上‘忘记’,而其内部结构几乎未变,那它随时可以恢复原样。"
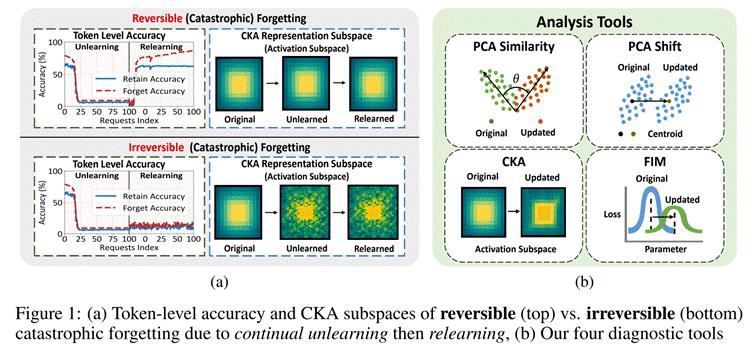
上图左侧(a)展示了两种典型遗忘场景:
上方:虽然 Unlearning 阶段准确率急剧下降,但 Relearning 之后快速恢复,表示空间保持稳定,属于可逆(灾难性)遗忘;
下方:虽然行为表现下降,但结构严重扰动,重训练也难以恢复,属于不可逆(灾难性)遗忘。
右侧(b)则展示了我们构建的表示空间分析工具,包括:
PCA Similarity/Shift
CKA 相似性分析
Fisher 信息矩阵(FIM)
表征空间分析揭示了 " 遗忘的可逆边界 "
研究者在 Yi-6B 模型上对不同方法(GA, GA+KL, NPO, RLabel)进行了单次遗忘实验,比较了三种指标:
MIA:攻击者能否识别遗忘目标是否出现过;
F.Acc:遗忘样本的准确率;
R.Acc:保留样本的准确率。
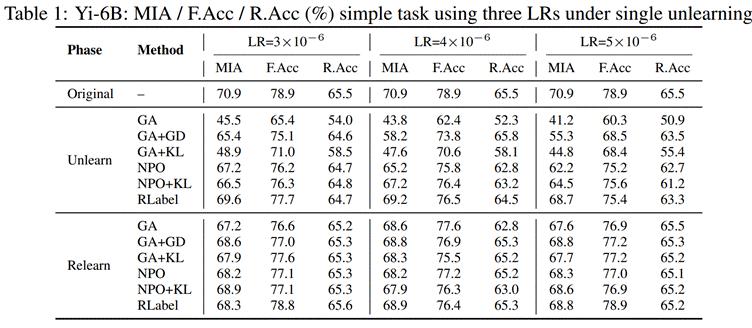
△在不同学习率下,多种方法的单次遗忘结果对比
进一步,研究者探究了不同请求数量(N)和学习率(LR)组合下的变化:
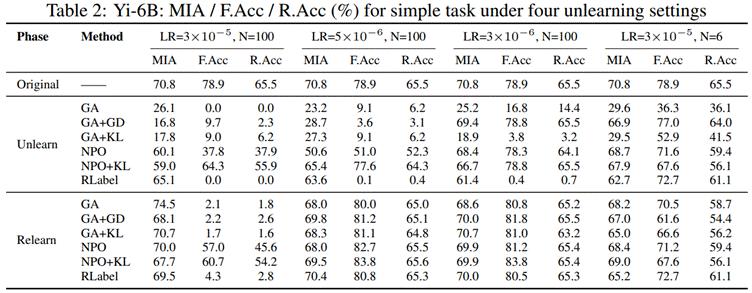
上图为在持续遗忘场景下,更大规模的遗忘实验配置(N × LR 组合)下的性能波动。
可视化诊断:模型真的 " 忘记 " 了吗?PCA Similarity:衡量表示空间主方向变化
研究者发现,对于可逆性遗忘,其表示空间在 Relearning 后高度恢复原始主方向,而不可逆性遗忘则呈现广泛漂移:
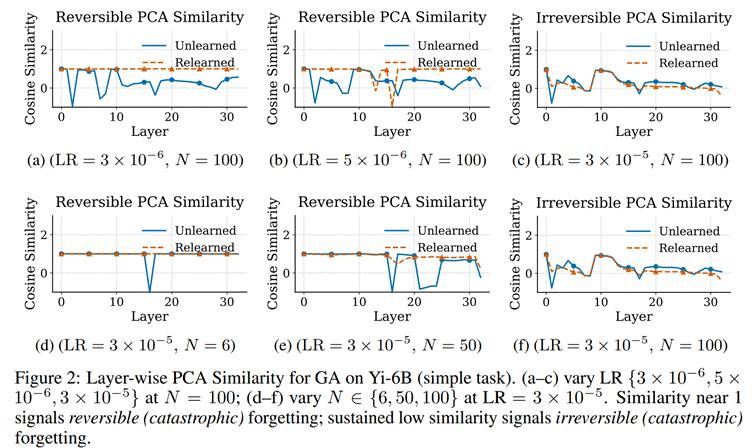
△各层 PCA 主方向变化(Cosine 相似度)分析 PCA Shift:量化表示分布中心的偏移程度
对于不可逆性遗忘,其 " 表示漂移 " 不仅方向变化,更伴随大尺度的空间位移,Relearning 难以还原:
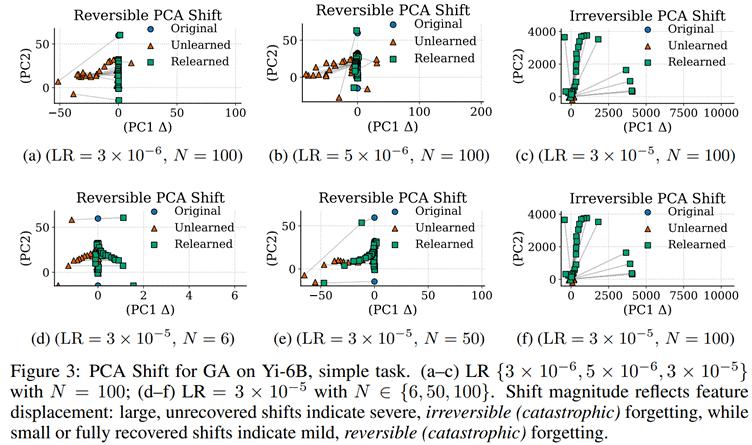
△各阶段的 PCA 散点漂移示意图 CKA:表示空间结构相似性分析
Linear CKA 揭示了各层之间的结构保留程度。可逆性场景下,CKA 几乎未受破坏,而不可逆性场景则迅速退化为低相关结构:
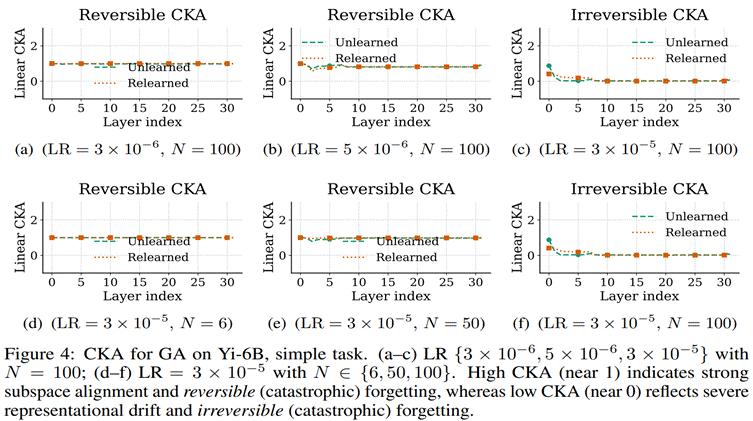
△CKA 曲线分析(逐层)Fisher 信息矩阵:重要参数的扰动程度
FIM 从参数空间的角度提供了视角。研究人员聚焦 Layer 31,观察其 Fisher 分布是否仍保留原始结构。
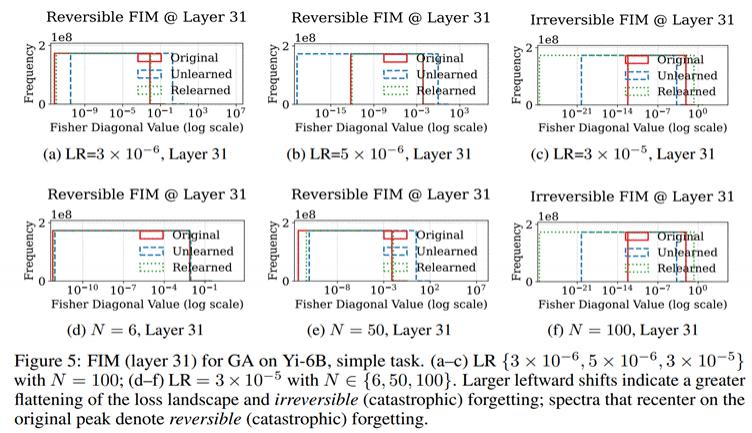
更复杂任务:可逆性能否扩展至复杂任务?
在 Qwen2.5-7B 上,研究者扩展实验至 MATH 和 GSM8K 推理任务。尽管任务复杂,他们依然观察到 " 受控 Relearning" 可带来准确率恢复,尤其在可逆场景中甚至超越初始性能。
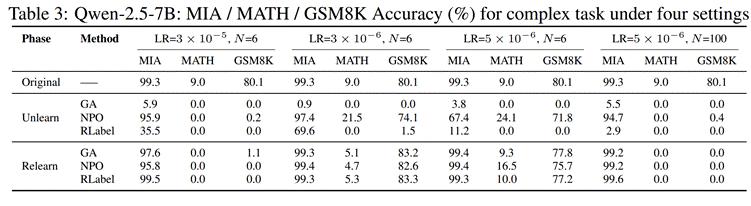
△MATH 与 GSM8K 任务下各方法表现对比结论
研究者从结构层面系统剖析了大模型遗忘的可逆性,得出以下核心结论:
持续遗忘风险远高于单次操作,GA/RLabel 破坏性强
单次遗忘多数可恢复,而持续性遗忘(如 100 条请求)易导致彻底崩溃。GA、RLabel 易过度遗忘,GA+KL、NPO 类方法能显著提高稳定性。
真正的遗忘表现为结构漂移而非输出下降
不可逆遗忘伴随 PCA 主方向旋转、分布漂移、Fisher 质量下降;仅凭 token-level 指标难以揭示这种深层变化。
遗忘可能带来隐式增强效果
在部分场景中,Relearning 后模型对遗忘集的表现优于原始状态,提示 Unlearning 可能具有对比式正则化或课程学习效果。
结构诊断工具支持可控性遗忘设计
PCA/CKA/FIM 不仅揭示是否崩溃,更可定位破坏位置,为实现 " 可控、局部、不可逆 " 的安全遗忘机制奠定基础。
本工作由 Xiaoyu Xu, Xiang Yue, Yang Liu, Qingqing Ye, Haibo Hu, Minxin Du 共同完成。
论文地址:https://arxiv.org/abs/2505.16831
Github 地址:https://github.com/XiaoyuXU1/Representational_Analysis_Tools.git
一键三连「点赞」「转发」「小心心」
欢迎在评论区留下你的想法!
— 完 —
点亮星标
科技前沿进展每日见